SEMANA #1 (8-11) JUNIO
En esta semana adquirimos los siguientes conocimientos
Incrementos y diferenciales
Mediante análisis gráfico y matemático es posible determinar el valor de un incremento de una función tanto en el eje x , como en el y, recordando que si se trata de una función linealmente homogénea, el incremento se realizará de manera simétrica tanto en x como en y, razón por la cual hemos separado en un valor real y un valor aproximado
Parte del estudio de las funciones de varias variables es indispensable identificar el número de variables, que dicha función posee, ahora en el estudio de derivación y diferenciación, tomamos en cuenta funciones de dos y tres variables por lo general. En cursos anteriores se había aprendido a derivar funciones con respecto a una sola variable independiente, nosotros vamos mantener el mismo concepto tomando en cuenta que el resto de variables que no corresponden a la derivación son valores constantes.
La derivación y diferenciación, pueden realizarse por múltiples veces , tantas veces lo permita la función, ya que se trabaja con funciones de multiples variables es posible obtener derivadas y diferenciales de cada una de las variables presentes en la función teniendo segundas, terceras, cuartas,...., derivadas y segundos, terceros, cuartos diferenciales, ya que las propiedades y artificios son similares para la derivación como para la diferenciación.
Para determinar una derivada direccional consideramos el vector gradiente, mismo que se puede obtener al derivar parcialmente una función escalar para cada una de las componentes de un vector, que estaría dado por x, y , z. Una derivada direccional se define como el producto del vector gradiente por el unitario del vector en el cual estará orientada la derivada.
PLANOS TANGENTES Y RECTA NORMAL UNA SUPERFICIE
Para mayor comprensión de conocimientos teóricos y ejercicios, haz clic aqui.
Máximos y mínimos
Si f está una función de x y y, entonces f tiene un máximo relativo a (a, b) si f(a, b) ³ f(x,y) para toda (x, y) en una pequeña cercanía de (a, b). Un mínimo relativo se define en manera parecida. f tiene un punto de silla en (a, b) si f tiene allí un mínimo relativo a lo largo de un corte y un máximo relativo a lo largo de un otro corte.
La función que se ilustra mas abajo tiene un mínimo relativo a (0, 0), un máximo relativo a (1, 1), y puntos de silla a (1, 0) y (0, 1).
En los casos que estudiamos, todos extremos relativos y puntos de silla que no sean en la frontera del dominio de f se ocurren a puntos críticos, que son las soluciones de las ecuaciones
fx(x,y) = 0 Y fy(x,y) = 0.
CRITERIO DE LA SEGUNDA DERIVADA
Si f(x, y) está una función de dos variables, y (a, b) es un punto crítico de f. (Esto es, fx(a, b) = 0 y fy(a, b) = 0.) Suponga también que existen y son iguales las derivadas del segundo orden, de modo que, por teoremas de cálculo, fxy es igual a fyx. Sea
H = fxx(a, b)fyy(a, b) -[fxy(a, b)]2.
Entonces
- f tiene un mínimo relativo a (a, b) si H > 0 y fxx(a,b) > 0,
- f tiene un máximo relativo a (a, b) si H > 0 y fxx(a,b) < 0, y
- f tiene un punto de silla a (a, b) si H < 0.
Sea f(x, y) = x2 - (y-1) 2. Entonces fx(x,y) = 2x; fy(x, y) = -2(y-1). Para encontrar los puntos críticos, resolvemos la sistema
- 2x = 0
- -2(y-1) = 0
Para comprobar cual, calcule primero las derivadas segundas:
fxx(x, y) = 2
fyy(x, y) = -2
fxy(x, y) = fyx(x, y) = 0
Después calcule
H = fxx(0, 1)fyy(0, 1) -[fxy(0, 1)]2
= (2)(-2) -02 =- 4
Como H es negativo, tenemos un punto de silla a (0, 1). Aquí está la gráfica de f que muestra su ubicación.
Máximos y mínimos absolutos
Un problema restringido de optimización Tiene la formaMaximiza (o minimiza) f(x, y,. . . ) sujeta a restricciones.Las restricciones están en forma de ecuaciones o en forma de restricciones del dominio de f.
Podemos resolver estos problemas por primero despejar una de las variables de las ecuaciones de restricción, para después sustituirla en f, y después ubicar el máximo (o mínimo) de la función que resulta. En casos en los que el dominio R de la función resultando tiene una frontera, tenemos también ubicar los extremos de f cuando se está restringido a la frontera.
Multiplicadores de Lagrange

Consideremos un caso bidimensional. Supongamos que tenemos la función, f (x, y), y queremos maximizarla, estando sujeta a la condición:

donde c es una constante. Podemos visualizar las curvas de nivel de f dadas por

Una vez determinados los valores de λ, volvemos al número original de variables y así continuamos encontrando el extremo de la nueva ecuación no restringida.
 de forma tradicional. Eso es,
de forma tradicional. Eso es,  para todo (x, y) satisfaciendo la condición porque
para todo (x, y) satisfaciendo la condición porque  es igual a cero en la restricción, pero los ceros de
es igual a cero en la restricción, pero los ceros de  F(x, y) están todos en
F(x, y) están todos en 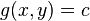 .
.
SEMANA #2 (15-18) JUNIO
En el capítulo pasado habíamos definido que era un vector gradiente, bueno pues ahora utilizaremos el vector gradiente de una función, el mismo que va a ser igualado a lamda multiplicado por el vector gradiente de una función de enlace, para operar se necesita despejar lamda y obtener los valores o puntos críticos, el calculo de dichos puntos tiene que ver mucho con las posibles aplicaciones de los multiplicadores de Lagrange para la optimización de superficies, volumenes, perímetros, etc.
Parte del estudio de las funciones vectoriales es determinar el volumen bajo la curva, tomando en cuenta un plano de referencia, en este caso sera el XY. Al mencionar volumen, tenemos que considerar las tres dimensiones de las cuales depende, es por este que realizar una integral lineal no seria suficiente para determinar el volumen, ahora aplicaremos integrales múltiples en las que se destacan las integrales de Área o integral doble y de Superficie o integral triple, el método mas fiables es considerar un diferencial dependiendo del caso.
Integral dobleLa integral doble de f(x, y) en la región R del plano xy se define como
= Volumen arriba de la región R y abajo de la gráfica de f
- Volumen abajo de la región R y arriba de la gráfica de f.
La siguiente figura demuestra el volumen (en el caso que la gráfica de f está arriba de la región R).

Si R es el rectángulo a ≤ x ≤ b y c ≤ y ≤ d (vea la figura más abajo) entonces

Si R es la región a ≤ x ≤ b y c(x) ≤ y ≤ d(x) (como se demuestra en la figura más abajo) entonces se calcula la integral en R con la siguiente ecuación:

Si R es la región c ≤ y ≤ d y a(y) ≤ x ≤ b(y) (como se demuestra en la figura más abajo) entonces se calcula la integral en R con la siguiente ecuación:

Transformación de integrales múltiples
En un espacio R2, un dominio de integración que tenga una simetría circulares. Donde cada punto P (x, y) del dominio de una integral doble tomará su valor correspondiente en coordenadas polares mediante la siguiente transformación:


El determinante jacobiano de la transformación es:

El cual se obtiene insertando las derivadas parciales de x = ρ cos(θ), y = ρ sin(θ) en la primera columna con respecto a ρ y en la segunda con respecto a
 .
.Por lo tanto, una vez transformada la función, y multiplicada por su determinante jacobiano, ésta es igual a la integral original:

Coordenadas Cilíndricas
El uso de coordenadas cilíndricas para transformar una integral triple, es conveniente especialmente cuando el dominio de integración presenta simetría alrededor del eje z. La función se transforma mediante la siguiente relación.


El determinante jacobiano de la transformación es el siguiente:
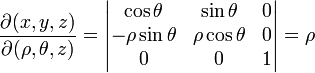
Por lo tanto, se puede derivar la siguiente fórmula de integración:

Coordenadas Esféricas
Cuando existe simetría esférica en un dominio en R3, es posible utilizar una transformación hacia coordenadas esféricas para simplificar una integral triple. La función es transformada por la relación:
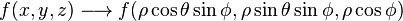
.svg%2F190px-Spherical_Coordinates_(Colatitude%252C_Longitude).svg.png&container=blogger&gadget=a&rewriteMime=image%2F*)
El determinante jacobiano de la transformación es el siguiente:
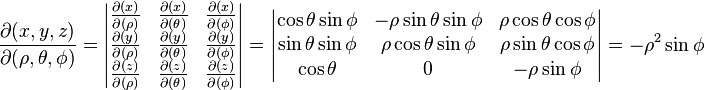
Tomando el valor absoluto del determinante se obtiene el factor que se debe añadir a la integral.
Por lo tanto los diferenciales dx dy dz se transforman en ρ2 sin(φ) dρ dθ dφ.
Finalmente se obtiene la fórmula de integración:

Para mayor comprensión de los conceptos teóricos y ejercicios, haz clic aqui.
SEMANA #3 (22-25) JUNIO
APLICACIONES DE LAS INTEGRALES MULTIPLES
Centro de masa

Para un sistema de masas discreto, formado por un conjunto de masas puntuales, el centro de masas se puede calcular como:

 ,
, masa total del sistema de partículas.
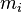 , masa de la partícula i-ésima.
, masa de la partícula i-ésima. , vector de posición de la masa i-ésima respecto al sistema de referencia supuesto.
, vector de posición de la masa i-ésima respecto al sistema de referencia supuesto.Distribución continua de materia
Para sistemas de masas continuos o distribuciones continuas de materia debemos recurrir al Cálculo Infinitesimal e Integral, de modo que la expresión anterior se escribe en la forma:

Distribución de masa homogénea
Si la masa está distribuida homogéneamente, la densidad será constante por lo que se puede sacar fuera de la integral haciendo uso de la relación siguiente:


siendo V el volumen total.
Para mayor comprensión de los conceptos teóricos y ejercicios, haz clic aqui.
29 DE JUNIO DEL 2015
Campos Vectoriales
Algunos conocimientos anteriores nos dan pautas a cerca de los campos vectoriales, podemos definir a un campo vectorial, a un vector que posee tres coordenadas, las cuales representan los ejes coordenados. Los campos vectoriales se pueden interpretar como la tendencia de una fuerza a lo largo de una superficie, en cada punto el valor del campo no puede otorgar una posible dirección en la cual el flujo, va a desplazarse.

Para f : R2 → R un campo escalar, la integral sobre la curva C (también llamada, integral de trayectoria), parametrizada como r(t)=x(t)i+y(t)j con t
 [a, b], está definida como:
[a, b], está definida como:

donde: r: [a, b] → C es una parametrización arbitraria de la curva C de tal manera que r(a) y r(b) son los puntos finales de C. Las integrales de trayectoria son independientes de la parametrización r(t), porque solo depende de la longitud del arco, también son independientes de la dirección de la parametrización r(t).











No hay comentarios:
Publicar un comentario