9 de Abril
El 9 de abril empezamos con el tema de GEOMETRIA EN EL ESPACIO, es decir en R2 y en R3. Para lo cual debimos primero abordar lo que son la funciones implicitas.
GEOMETRIA EN EL ESPACIO
En R2 : ES una funcion implicita de dos variables F(x,y)=0 y en este se pueden dar dos casos
1er CASO: Y= f(x), en donde (Y) es la variable dependiente y (X) es la variable independiente.
2do CASO: X=f(y), en donde (X) es la variable dependiente y (Y) es la variable independiente.
* Goemetricamente F(x,y) representa en R2 una CURVA en el plano.
* EL SISTEMA DE ESTAS FUNCIONES. Nos da uno o mas puntos dependiendo de las funciones.
En R3 : esta es una funcion implicita con tres variables F(x,y,z)=0 y en este se pueden dar tres casos.
CASO 1: Z=f(x,y); en donde (Z) es la variable dependiente y (X,Y) son las variables independientes.
CASO 2: Y=g(x,z); en donde (Y) es la variable dependiente y (X,Z) son las variables independientes.
CASO 3: X=h(y,z); en donde (X) es la variable dependiente y (Y,Z) son las variables independientes.
CASO ESPECIAL: F(X,Y)=0: Esta es una funcion implicita que representa en R3 una superficie con generatriz paralela al eje OZ .
* Geometricamente la interseccion de dos funciones en R3 nos representa curva.
* Geometricamente la interseccion de tres funciones implicitas en R3 nos da un punto en R3.
En esta semana empezamos determinando las ecuaciones para obtener la ecuacion de una recata dados varios parametros por ejemplo:
para ampliar mejor los conocimientos clic aqui
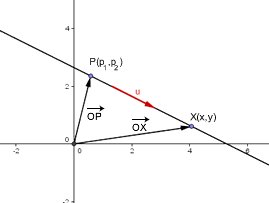
Dados dos puntos y apoyandonos del analisis grafico y matematico podemos llegar a determinar la ecuacion de la recta.La misma que al inicioo va ser representada de forma vectorial, pero despues mediante susutituciones podemos llegara las ECUACIONES CARTESIANAS O CANONICAS.
Distancia de un punto a una recta
Mediante el análisis gráfico se puede determinar la distancia de un punto a una recta, mediante el concepto vectorial de una proyección de un vector sobre otro, siendo la respuesta una cantidad escalar con signo positivo.Para ampliar los conocimientos teóricos click aquí.
-El plano en tres dimensiones
Para determinar correctamente la Ecuación General del plano es necesario agrega un concepto nuevo, el vector normal(n) el mismo que por característica general es perpendicular al plano evaluado.Inicialmente se determina mediante un proceso de demostración la Ecuación Vectorial y después de realizar la respectiva sustitución de valores y realizar operaciones algebraicas se llega a una Ecuación General para el plano.
Para ampliar los conocimientos teóricos click aquí.
Ecuaciones incompletas del plano
Mediante análisis matemático se pudo determinar una relación entre la ecuación general del plano y sus diferentes componentes ( A, B, C ) en la ausencia de A, de B o de C la ecuación general del plano se ajusta a cada caso.
Para ampliar los conocimientos teóricos click aquí.
Mediante análisis matemático se pudo determinar una relación entre la ecuación general del plano y sus diferentes componentes ( A, B, C ) en la ausencia de A, de B o de C la ecuación general del plano se ajusta a cada caso.
Para ampliar los conocimientos teóricos click aquí.
Ecuación segmentaria del plano
Mediante análisis aritmético y lógico se pudo determinar una ecuación en la que los coeficientes de X, Y, Z dependen de una operación matemática en la que toda la ecuación general del plano es dividida para el coeficiente (-D). A ésta relación llamaremos Ecuación General del Plano.
Para ampliar los conocimientos teóricos click aqui.
Mediante análisis aritmético y lógico se pudo determinar una ecuación en la que los coeficientes de X, Y, Z dependen de una operación matemática en la que toda la ecuación general del plano es dividida para el coeficiente (-D). A ésta relación llamaremos Ecuación General del Plano.
Para ampliar los conocimientos teóricos click aqui.
Ecuación normal del plano
Partiendo de la ecuación general del plano y analizando sus coeficientes, se llega a determinar mediante operaciones vectoriales que existe un relación entre dichos coeficientes y los unitarios del vector normal, A=cos($) , B=cos(%) , C=cos(#) y D=-p.
Para ampliar los conocimientos teóricos click aqui.
Partiendo de la ecuación general del plano y analizando sus coeficientes, se llega a determinar mediante operaciones vectoriales que existe un relación entre dichos coeficientes y los unitarios del vector normal, A=cos($) , B=cos(%) , C=cos(#) y D=-p.
Para ampliar los conocimientos teóricos click aqui.
Plano determinado por tres puntos
Recordemos que mediante tres puntos, es posible encontar 2 vectores en un mismo punto de origen y mediante el producto cruz es fácil determinar el vector normal al plano. Todo el proceso se reduciría a uno antes analizado para determinar la ecuación general del plano.
Para ampliar los conocimientos teóricos click aqui.
BIBLIOGRAFIA:
Para el resumen de la presente se utilizo las siguientes fuentes :
http://www.vitutor.com/analitica/recta/ecuaciones_recta.htmlhttp://www.geoan.com/analitica/recta/vector_normal.html
http://www.vitutor.com/analitica/recta/ecuaciones_recta.html
https://docs.google.com/file/d/0B3NNTBVL1_YVZDR4ZUN5OEl6REU/edit?usp=drive_web (capitulo 12)
SEMANA #3 (20-23) ABRIL
TEMAS ESTUDIADOS DURANTE LA SEMANA
Haz de planos
Sabemos que todo plano puede rotar a través de un eje fijo, para este caso tomaremos una recta, de esta manera tendremos infinitos planos que se pueden intersecar en la misma curva. Mediante sus ecuaciones generales podemos deducir una ecuación general para el haz de planos formado.
Sabemos que todo plano puede rotar a través de un eje fijo, para este caso tomaremos una recta, de esta manera tendremos infinitos planos que se pueden intersecar en la misma curva. Mediante sus ecuaciones generales podemos deducir una ecuación general para el haz de planos formado.
Para ampliar los conocimientos teóricos click aquí.
Distancia de un punto a plano
Ecuación vectorial de la esfera
Mediante conocimientos anteriores, podemos relacionar la Ecuación Generalde la Esfera como una forma vectorial, para ello debemos considerar el centro o punto de origen, un vector director y un vector posición.
Para ampliar los conocimientos teóricos click aqui.
Mediante conocimientos anteriores, podemos relacionar la Ecuación Generalde la Esfera como una forma vectorial, para ello debemos considerar el centro o punto de origen, un vector director y un vector posición.
Para ampliar los conocimientos teóricos click aqui.
SUPERFICIES DE SEGUNDO ORDEN
Las superficies con las que trabajaremos en el curso se generan a partir de una curva que se mueve en el espacio (llamada generatriz). Trazar la gráfica de una superficie de este tipo es muy simple, la idea es arrastrar la generatriz en la dirección que se requiera, el movimiento de la generatriz forma la superficie por la traza que va dejando.
Para ampliar los conocimientos teóricos click aquí.
Las superficies con las que trabajaremos en el curso se generan a partir de una curva que se mueve en el espacio (llamada generatriz). Trazar la gráfica de una superficie de este tipo es muy simple, la idea es arrastrar la generatriz en la dirección que se requiera, el movimiento de la generatriz forma la superficie por la traza que va dejando.
Para ampliar los conocimientos teóricos click aquí.
ANALISIS DE LAS SUPERFICIES DE SEGUNDO ORDEN
Para poder graficar funciones llamadas superficies cuádricas, tales como con elipsoide, hiperboloides, paraboloides o cualquier otra superficie, nos apoyamos en un análisis, el mismo que cuenta con 3 simples paso;
1) Determinar la interacción con los ejes coordenados de la función a graficar
2) Determinar la intersección de la función con los planos coordenados
3) Determinar la intersección con los planos paralelos a los ejes coordenados.
Para poder graficar funciones llamadas superficies cuádricas, tales como con elipsoide, hiperboloides, paraboloides o cualquier otra superficie, nos apoyamos en un análisis, el mismo que cuenta con 3 simples paso;
1) Determinar la interacción con los ejes coordenados de la función a graficar
2) Determinar la intersección de la función con los planos coordenados
3) Determinar la intersección con los planos paralelos a los ejes coordenados.
EN EL SIGUIENTE VIDEO SE PUEDE OBSERVAR PARA TENER UN MAYOR CONOCIMIENTO DEL TEMA
SEMANA #4 (27-30) ABRIL
Funciones Vectoriales
Una función vectorial de variable vectorial es una regla que asocia a cada punto r de una cierta región n S ⊂ \ un vector m F(r) ∈ \ y se denota como : n m F S ∈ \ \ → Al conjunto S de valores que toma la variable independiente, se le denomina dominio y al conjunto de valores que toma F (r) se le llama imagen o recorrido. Las funciones vectoriales se conocen también como campos vectoriales y aquí se clasificarán en:
Una función vectorial de variable vectorial es una regla que asocia a cada punto r de una cierta región n S ⊂ \ un vector m F(r) ∈ \ y se denota como : n m F S ∈ \ \ → Al conjunto S de valores que toma la variable independiente, se le denomina dominio y al conjunto de valores que toma F (r) se le llama imagen o recorrido. Las funciones vectoriales se conocen también como campos vectoriales y aquí se clasificarán en:
- Campos vectoriales de variable escalar
- Campos vectoriales de variable vectorial
- Campos vectoriales de variable vectorial
De las funciones dadas, podemos realizar un análisis como por ejemplo:Límites, Continuidad, Derivadas, Integrales. También podemos realizar gráficos de apoyo en R2 en los que podemos determinar el dominio de la función.
Para ampliar los conocimientos teóricos click aquí.










No hay comentarios:
Publicar un comentario